PPO算法-chapter9-策略梯度方法

[chapter-9]-策略梯度方法

[PPO算法]-策略梯度-梯度上升和Reinfore

前言

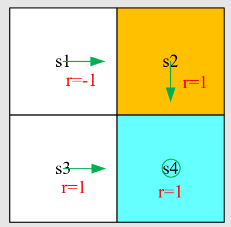
此前，策略一直以表格形式表示：

  • 所有状态的动作概率存储在一张表 中，表的每个条目由状态-动作对索引。
​ ​ ​ ​ ​
​ ​ ​ ​ ​ ​
​ ​ ​ ​ ​ ​
​ ​ ​ ​ ​ ​

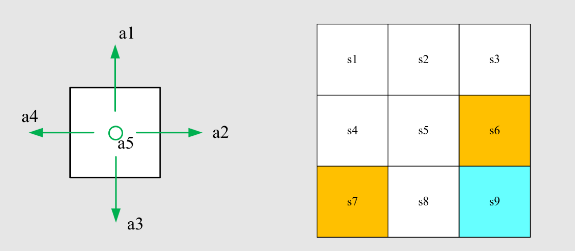
现在，策略也可以用带参数的函数表示：

其中 是参数向量。

  • 该函数可以是神经网络，输入为状态 ，输出为执行每个动作的概率，参数为 。
  • 优点：当状态空间很大时，表格表示在存储和泛化方面效率低下。
  • 函数表示有时也写作 、 或 。

表格表示与函数表示的差异：

首先，如何定义最优策略？

  • 在表格情形中，策略 最优当且仅当它能最大化每个状态的价值。
  • 在函数情形中，策略 最优当且仅当它能最大化某个标量指标。

其次，如何获取某个动作的概率？

  • 在表格情形中，可直接查表获得在状态 下采取动作 的概率。
  • 在函数情形中，需根据函数结构与参数 计算 的值。

策略梯度的基本思想很简单：

第一，定义最优策略的指标（或目标函数）：

用它来衡量策略的优劣。

第二，用基于梯度的优化算法搜索最优策略：

尽管思想简单，当我们试图回答以下问题时，复杂性便出现了：

  • 应该使用哪些合适的指标？
  • 如何计算这些指标的梯度？

本节课将详细解答这些问题。

目标函数的指标

第一个指标是平均状态价值，简称平均价值：

  • 是状态价值的加权平均。
  • 是状态 的权重。
    由于 ，我们可以将 理解为一种概率分布，因此该指标也可写作：

如何选择分布 ？有两种情况。

情况 1： 与策略 无关

  • 这种情况相对简单，因为指标的梯度更容易计算：

  • 此时，我们将 特别记为 ， 记为 。

如何选择 ​ ？

  • 一种简单方法是所有状态同等重要，即：

  • 另一种重要情况是只关心某个特定状态 。
    例如，某些任务的所有回合都从同一状态 开始，那么我们只关心从 出发的长期回报。此时：

    在这种情况下，。

情况 2： 依赖于策略 。

  • 常见做法是将 选为 ，即在策略 下的平稳分布。
    平稳分布的细节见上一节课及教材。

选择 的含义如下：

  • 反映了在给定策略 下，马尔可夫决策过程的长期行为。
  • 如果某个状态在长期中被频繁访问，则它更重要，应赋予更大权重；
  • 如果某个状态几乎不被访问，则赋予较小权重。

一个重要的等价表达式：

你将在文献中经常见到如下指标：

问题：它与我们刚才介绍的指标有什么关系？

回答：它们是同一个指标。原因在于：

第二个指标是平均一步奖励，简称平均奖励：

其中 ，，。

备注：

  • 是即时奖励的加权平均。
  • 是从状态 获得的平均即时奖励。
  • 是平稳分布。

一个重要的等价表达式：

  • 假设智能体遵循给定策略并生成一个轨迹，其奖励为 。
  • 该轨迹上的平均一步奖励为

其中 是轨迹的起始状态。

一个重要的事实是：

备注：

  • 强调：起始状态 不重要。
指标 表达式 1 表达式 2 表达式 3
​ ​ ​ ​
​ ​ ​ ​

表：对 和 不同但等价的表达式的总结

关于指标的备注 1：

  • 所有这些指标都是 的函数。
  • 由于 由 参数化，这些指标也是 的函数。
  • 换句话说，不同的 值可以产生不同的指标值。

因此，我们可以寻找最优的 值来最大化这些指标。
这是策略梯度方法的基本思想。

关于指标的备注 2：

  • 一个复杂之处在于，这些指标可以在折扣情况（）或非折扣情况（）下定义。

关于指标的备注 3：

  • 和 之间有什么关系？

  • 这两个指标是等价（但不相等）的。具体来说，在折扣因子 的折扣情况下，有：

因此，它们可以同时最大化。

目标函数梯度计算

给定一个指标，我们接下来

  • 推导其梯度
  • 然后应用基于梯度的方法优化该指标

梯度计算是策略梯度方法中最复杂的部分之一！原因在于

  • 首先，我们需要区分不同指标：、 等
  • 其次，我们需要区分折扣与非折扣情况

直接给出梯度表达式（无证明）：

上式是多种情形的统一表达式：

  • 可以是 、 或其他指标
  • “=” 可能表示严格相等、近似或成比例
  • 是状态的分布或权重

该表达式的推导非常复杂，此处不展开。感兴趣的读者可参考我的教材。
对大多数读者而言，记住此表达式即可。

梯度的紧凑且重要表达式：

首先，为何此表达式有用？

  • 因为我们可用样本近似梯度：

其中 为样本。这就是随机梯度下降的思想。

第二，如何证明上述等式？

证明：考虑自然对数函数 ，显然有

从而

于是有

备注：
为使 有定义，必须对任意 满足

  • 这可通过 softmax 实现，它能将任意实数向量归一化为分量在 且和为 1 的概率分布。
    例如，对向量 ，

  • 具体地，策略函数取形式

    其中 为待学习的函数。

备注：

  • 这种基于 softmax 的形式可由一个神经网络实现，其输入为状态 ，参数为 。网络输出维度为 ，每个输出对应一个动作 的策略概率 ，输出层激活函数需使用 softmax。
  • 由于对所有 均有 ，该参数化策略是随机的，因而具有探索性。
  • 也存在确定性策略梯度（DPG） 方法

基于梯度的算法和Reinfore

现在，我们给出第一个策略梯度算法来寻找最优策略！

  1. 最大化 的梯度上升算法：

  1. 由于真实梯度未知，可用随机梯度代替：

  1. 进一步， 也未知，可用其估计 替代：

若用 蒙特卡洛估计 来计算 ，该算法有一个专门的名字：

REINFORCE

  • REINFORCE 是最早且最简单的策略梯度算法之一。
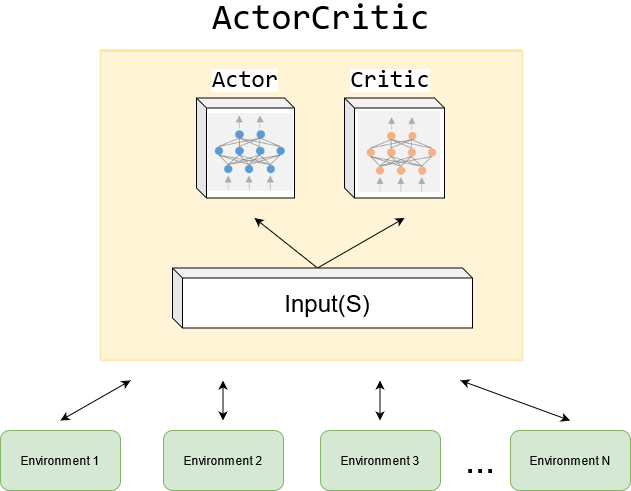
  • 许多其他策略梯度算法（如下一讲将介绍的 Actor-Critic 方法）都可看作是对 REINFORCE 的扩展。

伪代码：蒙特卡洛策略梯度（REINFORCE）

初始化：初始参数 ；；。
目标：学习最优策略以最大化 。

对每个回合，执行：

  1. 依照 生成一个回合

  2. 对于 ：

    • 价值更新：
    • 策略更新：

备注 1：如何进行采样？

  • 如何采样状态 ​ ？
    ，其中 是在策略 下的长期行为分布。
    实践中，人们通常不关心这一点。
  • 如何采样动作 ​ ？
    。因此， 应按照 在 处采样。
    因此，策略梯度方法是 on-policy 的。

备注 2：如何解释该算法？

由于

算法可重写为

因此，算法的重要表达式为

解释（续）： 可平衡探索与利用，原因如下：

  1. 与 成正比
    更大的 更大的 更大的
    因此算法倾向于利用价值更高的动作。
  2. 与 成反比（当 时）
    更小的 更大的 更大的
    因此算法倾向于探索概率较低的动作。

伪代码：蒙特卡洛策略梯度（REINFORCE）

初始化：
参数化策略 ，折扣因子 ，学习率 。

目标：寻找最优策略以最大化 。

第 次迭代，执行：

  1. 选取初始状态 ，依照 生成一条轨迹：
    。

  2. 对于 ，执行
    策略更新：

    其中 。

  3. 令 。

​

‍