PPO算法-chapter8-值函数近似和DQN
PPO算法-chapter8-值函数近似和DQN
Bohao Zhao[chapter-8]-值函数近似
[PPO算法]-值函数近似和DQN
前言
迄今为止,本书中状态值与动作值均用表格表示。
例如,动作值:
例如,状态值:
| 状态 | 值 |
|---|---|
优点:直观且易于分析。
缺点:难以处理大规模或连续的状态或动作空间,主要体现在两个方面:
- 存储:表格大小随状态/动作数量线性增长,内存开销大;
- 泛化能力:无法对未见过的状态或动作进行合理估值。
考虑一个例子:
- 有
个状态: 。 - 这些状态在策略
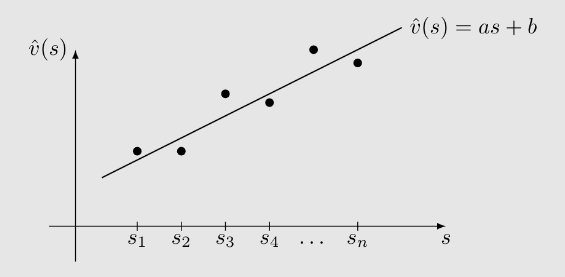
下的值为 。 非常大! - 我们希望用一条简单的曲线来近似这些值。
例如,可以使用支线来拟合这些点:

设这条直线的方程为
其中
为参数向量; 为状态 的特征向量; 对 是线性的。
表格法与函数法的区别:
如何获取一个状态的值
- 表格表示:直接从表格中读取对应状态的值。
- 函数表示:需将状态索引
输入函数,通过计算得到函数值。
例如,
- 优点:存储。我们不需要存储
个状态值。只需存储低维的 。
好处并非没有代价。它有一个代价:状态值不能准确表示。这就是为什么这种方法被称为近似。
我们可以使用高阶曲线更精确地拟合点:
在这种情况下:
- 尽管
总结:
思想:使用参数化函数近似状态和动作值:
关键区别:如何获取和改变
优点:
- 存储:
- 泛化能力:当访问状态
- 存储:
原理、目标函数
更正式介绍:
- 令
- 我们的目标是找到最优
- 这是一个策略评估问题。稍后将扩展到策略改进。
找到最优
- 定义目标函数。
- 推导优化目标函数的算法。
目标函数是
我们的目标是找到最优
期望是关于随机变量
- 这是新的。我们尚未讨论过状态的概率分布。
- 有多种定义
第一种方法是使用均匀分布。
- 即通过将每个状态的概率设为
- 在这种情况下,目标函数变为
缺点:
- 状态可能并不同等重要。例如,某些状态可能很少被策略访问。因此,这种方法未考虑给定策略下马尔可夫过程的真实动态。
第二种方法是使用平稳分布。
- 这是一个重要概念:描述马尔可夫过程在给定策略
- 令
- 目标函数可重写为
该函数是加权平方误差。
- 由于更频繁访问的状态
关于平稳分布的更多解释:
- 分布:状态分布
- 平稳:长期行为
- 总结:在agent长时间运行后,agent在任何状态的概率可由该分布描述。
备注:
- 也称为稳态分布或极限分布。
- 对理解值函数方法至关重要。
- 对下一讲中策略梯度量方法也很重要。
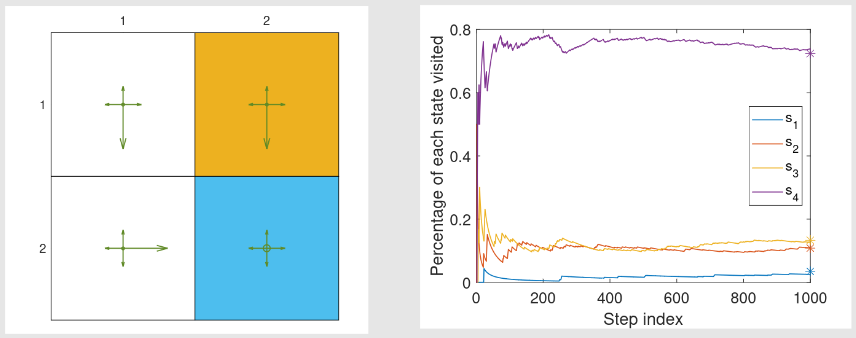
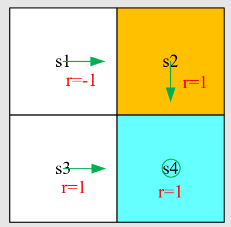
示例:
- 给定策略如图示。
- 令
- 则
收敛值可以预测,因为它们是
在这个例子中,
可以计算出特征值为 1 的左特征向量为
优化算法
虽然我们有目标函数,下一步是优化它。
为了最小化目标函数
真实梯度为
我们可以用随机梯度代替真实梯度:
其中
- 样本期望满足平稳分布。在实践中,可能不满足。
- 该算法不可实现,因为需要真实状态值
- 可以用近似
特别是,
首先,蒙特卡洛学习与函数近似:
为 从 开 始 的 折 扣 回 报 。 然 后 , 可 近 似 TD 学习与函数近似
伪代码:TD 学习的状态值函数近似
初始化:函数
可微分 。初始参数 。
目标:学习给定策略的真实状态值。 对于每个由
生成的 episode ,执行以下步骤: 对于每个样本
,执行 一般情况,
线性情况,
它只能估计给定策略的状态值,但理解后续算法重要。
拟合函数的选择
一个未回答的重要问题:如何选择函数
第一种广泛使用的方法是线性函数:
现在广泛使用的方法是神经网络作为非线性函数近似器。
- 例如,输入为
- 例如,输入为
在线性情况下
将梯度代入 TD 算法
得
这是线性函数近似的 TD 学习算法。课程中称为 TD-Linear。
线性函数方法的缺点:
- 难以选择合适的特征向量。
线性函数方法的优点:
- TD 算法在线性情况下的理论性质比非线性情况更易理解。
- 线性函数近似在表格表示是线性函数表示的特例中仍有效。
回顾 TD- TD-Linear 算法是
当
这是一个仅更新
方程两边同乘
即表格 TD-Table 算法(此处称为 TD-Table)。
总结:选择特例特征向量,TD-Linear 变为 TD-Table。
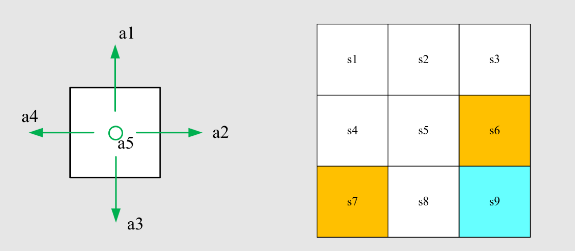
例子:考虑如下的网格世界
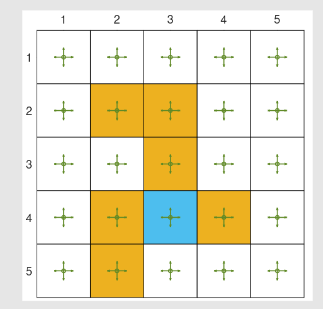
- 给定策略:
- 目标是估计该策略的状态值(策略评估问题)。
- 共有 25 状态值。接下来展示可用少于 25 参数近似 25 状态值。
- 设
,
求解贝尔曼公式得到的真值如下:
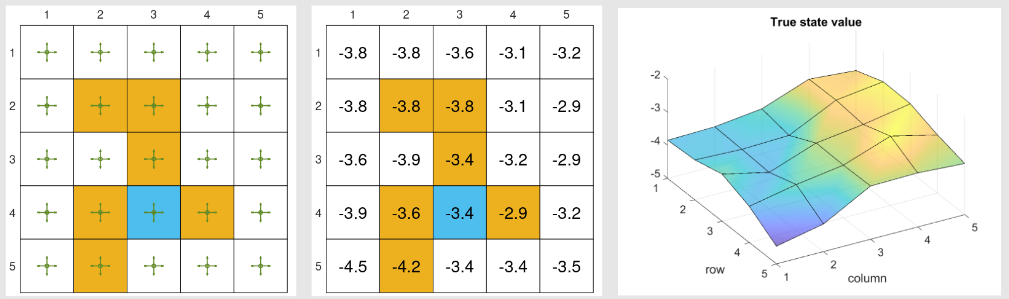
经验样本:
- 500 根据给定策略生成 500 个 episode。
- 每个 episode 500 步,从随机选择状态-动作对开始,遵循均匀分布。
用TD-table求得的如下所示
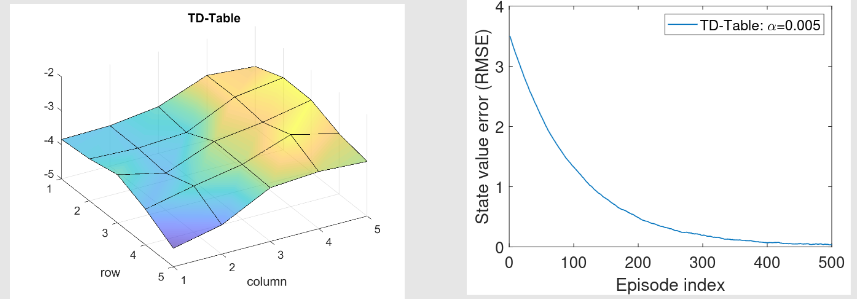
TD-Linear:
● 如何应用 TD-Linear 算法?
- 特征向量选择?
- 在这种情况下,近似的状态值为
备注:
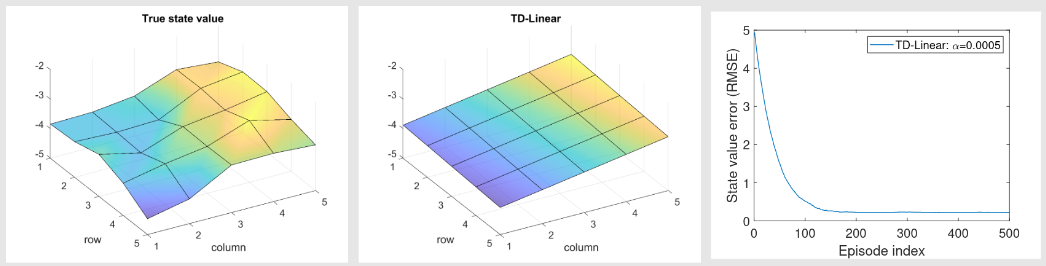
为了增强近似能力,我们可以使用高阶特征向量,从而引入更多参数。
- 例如,我们可以考虑
在这种情况下,
这对应于一个二次曲面。
- 我们可以进一步增加特征向量的维度:
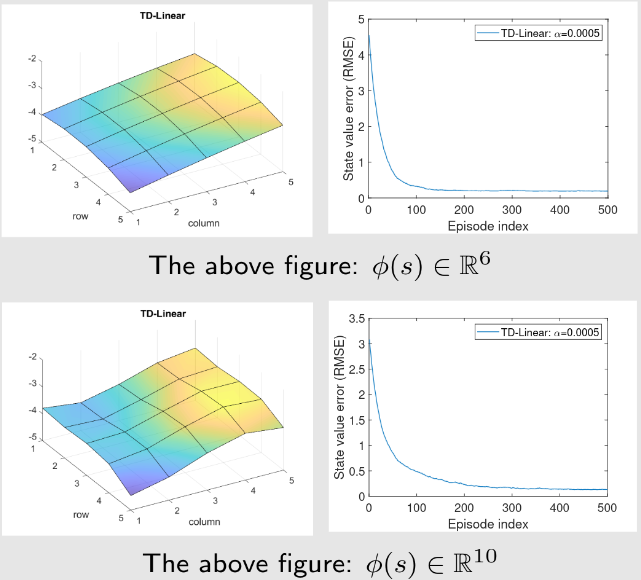
到目前为止,我们已经完成了关于价值函数近似的TD学习的故事。
- 这个故事从目标函数开始:
目标函数表明这是一个策略评估问题。
- 梯度下降算法是
- 真实价值函数是未知的,在算法中被一个近似所替代,导致算法:
虽然这个故事对于理解基本思想非常有帮助,但它在数学上并不严谨。
不同的目标函数:
- 目标函数 1:真实价值误差
- 目标函数 2:Bellman 误差
其中
- 目标函数 3:投影 Bellman 误差
其中
- TD-Linear 算法最小化投影 Bellman 误差。
带函数估计的sarsa
到目前为止,我们仅仅考虑了状态价值估计。即
为了搜索最优策略,我们需要估计动作价值。
具有价值函数近似的Sarsa算法是
这与我们在本讲座中先前介绍的算法相同,只是将
伪代码:具有函数近似的Sarsa
初始化:初始参数
。初始策略 。 对于所有 。 。
目标:学习一个最优策略,使代理从初始状态到达目标状态。
对于每个回合,执行以下操作:
根据
在 生成 如果
不是目标状态,则
根据
收集经验样本 :通过与环境交互生成 ;根据 生成 更新
-值(更新参数):
更新策略:
如 果
否 则
DQN
先回顾一下Q-learning:
类似于Sarsa,表格Q学习也可以扩展到值函数逼近的情况
Q值更新规则是
这与Sarsa相同,只是
伪代码:使用函数逼近的Q学习(策略版本)
初始化:初始参数
。初始策略 。 对于所有 。 。 目标:学习一条从初始状态
引导代理到目标状态的最优路径。 对于每个回合,做
如果
不是目标状态,做 收集经验样本
给定 :生成 遵循 ;通过与环境交互生成 。 更新值(更新参数):
更新策略:
如果
否则
Deep Q-learning 或 深度Q网络 (DQN):
引入深度神经网络到强化学习(RL)的最早和最成功的算法之一。
神经网络的作用是作为非线性函数逼近器。
与以下算法不同:
因为训练网络的方式不同。
深度Q学习旨在最小化目标函数/损失函数:
其中
如何最小化目标函数?梯度下降!
- 如何计算目标函数的梯度?很棘手!
- 这是因为,在这个目标函数中
参数
- 由于最优的
- 为了解决这个问题,我们可以在计算梯度时假设
为此,我们可以引入两个网络:
- 一个是主网络,表示
- 另一个是目标网络
此时,目标函数简化为:
其中
当
深度 Q 学习的基本思想是使用梯度下降算法来最小化目标函数。
- 然而,这样的优化过程涉及一些重要技巧,值得特别关注。
技巧 1:两个网络,一个主网络和一个目标网络
为什么使用它?
- 数学原因已在计算梯度时解释过。
实现细节:
设
在每次迭代中,我们从经验回放池(稍后解释)中抽取一个小批量样本
对于每个
因此,我们获得一个小批量数据:
使用
技巧 2:经验回放
问题:什么是经验回放?
回答:
在我们收集了一些经验样本之后,不按照它们被收集的顺序使用这些样本。
而是将它们存储在一个集合中,称为经验回放池:
每当我们训练神经网络时,可以从经验回放池中随机抽取一个小批量样本。
这种样本抽取方式称为经验回放,应遵循均匀分布。
问题:为什么深度 Q 学习中必须使用经验回放?为什么回放必须服从均匀分布?
回答:答案在于目标函数
假设状态-动作对
- 为什么是均匀分布?因为没有先验知识。
- 能否像以前一样使用平稳分布?不行,因为没有给定策略。
回答(续) :
- 然而,样本并不是均匀收集的,因为它们是由特定策略依次生成的。
- 为了打破连续样本之间的相关性,我们可以使用经验回放技术,从回放池中均匀抽取样本。
- 这就是经验回放必须采用均匀分布的数学原因,也是经验回放必不可少的根本原因。
回顾表格型情形
问题:为什么表格型 Q 学习不需要经验回放?
回答:因为它对状态
问题:为什么深度 Q 学习涉及分布?
回答:因为我们需要定义一个标量目标函数
其中期望
- 表格型情形的目标是为所有
- 而深度情形的目标是优化一个标量目标函数。
问题:表格型 Q 学习可以使用经验回放吗?
回答:可以,而且这样做样本效率更高(为什么?)。
伪代码:深度 Q 学习(离策略版本)
初始化:主网络与目标网络使用相同的初始参数。
目标:利用给定行为策略生成的经验样本,学习一个最优目标网络来近似最优动作价值。 将
生成的经验样本存入回放池
对于每次迭代,执行:
从
中均匀抽取一个小批量样本; 对每个样本
,计算目标值
其中
为目标网络参数; 利用该小批量样本,更新主网络以最小化
每
次迭代,执行
备注:
- 为什么没有策略更新?
- 网络的输入输出与 DQN 论文略有不同。
示例说明
- 我们需要为每个状态-动作对学习最优动作价值。
- 一旦获得最优动作价值,即可立即得到最优贪婪策略。
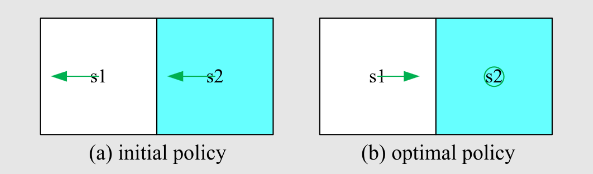
实验设置:
- 仅使用一个回合的数据来训练网络。
该回合由图 (a) 所示的探索性行为策略生成。 - 该回合仅有 1,000 步!而表格型 Q 学习需要 100,000 步。
- 使用一个浅层神经网络(单隐藏层)作为
- 详细内容见书籍。