PPO算法-chapter4-值迭代和策略迭代
PPO算法-chapter4-值迭代和策略迭代
Bohao Zhao[chapter-4]-值迭代和策略迭代
[PPO 算法]-基于模型的算法-值迭代和策略迭代
值迭代(Value Iteration)
如何解决贝尔曼最优方程?
压缩映射定理提出了一种迭代算法:
其中
接下来研究这种算法的实现,其可以分解为两个步骤。
- 步骤1:策略更新。这一步是求解
其中
- 步骤2:值更新。
问题:
策略更新
逐元素形式的
是
解决上述优化问题的最优策略是
其中
值更新
逐元素形式的
是
由于
根据上面的步骤,可以得到如下的伪代码
伪代码:值迭代算法
初始化:已知所有
的概率模型 和 。初始猜测 。 目标:搜索解决贝尔曼最优方程的最优状态值和最优策略。
当
未收敛,即 大于预定义的小阈值时,对于第 次迭代,执行以下操作:
对于每个状态
,执行以下操作:
对于每个动作
,执行以下操作: 计算
-值: 计算最大动作值:
策略更新:如果
,则 ,否则 值更新:
策略迭代(Policy Iteration)
算法描述:
给定一个随机初始策略
步骤1:策略评估(PE)
这一步是计算的状态值: 注意
是一个状态值函数。 步骤2:策略改进(PI)
最大化是逐元素进行的!
由算法得到一个序列
PE = 策略评估,PI = 策略改进
问题1:在策略评估步骤中,如何通过求解贝尔曼方程得到状态值
- 闭式解:
- 迭代解:
策略迭代是一种迭代算法,其中另一个迭代算法嵌入在策略评估步骤中!
问题2:在策略改进步骤中,为什么新的策略
引理(策略改进)
如果
,那么对于任意 ,有 。
问题3:为什么这样的迭代算法最终能够达到最优策略?
由于每次迭代都会改进策略,我们知道
因此,
定理(策略迭代的收敛性)
由策略迭代算法生成的状态值序列
收敛到最优状态值 。因此,策略序列 收敛到最优策略。
如何实现策略迭代算法?
策略评估具体步骤
矩阵-向量形式:
逐元素形式:
停止条件:当
策略上升步骤
矩阵-向量形式:
逐元素形式:
这里,
那么,贪心策略是
伪代码:策略迭代算法
初始化:已知所有
的概率模型 和 。初始猜测 。 目标:搜索最优状态值和最优策略。
当
未收敛时,对于第 次迭代,执行以下操作: 策略评估:
初始化:任意初始猜测当
未收敛时,对于第 次迭代,执行以下操作: 对于每个状态
,执行以下操作:
策略改进:
对于每个状态
,执行以下操作: 对于每个动作
,执行以下操作:
- 计算
-值: - 计算最大动作值:
- 策略更新:如果
,则 ,否则
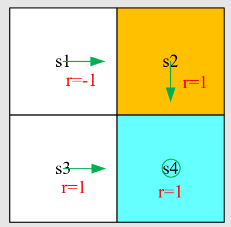
例:

- 奖励设置为
- 动作:
- 目标:使用策略迭代找出最优策略。
开始求解
迭代
直接求解方程:
迭代求解方程。选择初始猜测为
…继续迭代求解得
迭代
代入
通过寻找
这个策略经过一次迭代后就是最优的!在编程中,应继续直到满足停止条件。
截断策略步骤
一句话说:是上述策略的广义情况
先简单回顾之前的两种迭代方法
策略迭代:从
- 策略评估(PE):
- 策略改进(PI):
值迭代:从
- 策略更新(PU):
- 值更新(VU):
这两个算法非常相似:
策略迭代:
值迭代:
PE = 策略评估。PI = 策略改进。PU = 策略更新。VU = 值更新。
- 让我们仔细比较这些步骤:
| 步骤 | 策略迭代算法 | 值迭代算法 | 注释 |
|---|---|---|---|
| 1) 策略: | N/A | ||
| 2) 值: | |||
| 3) 策略: | 两种策略相同 | ||
| 4) 值: | |||
| 5) 策略: | |||
| … | … | … | … |
它们从相同的初始条件开始。
前三个步骤相同。
第四步变得不同:
- 在策略迭代中,求解
- 在值迭代中,
- 在策略迭代中,求解
考虑求解
值迭代
截断策略迭代
策略迭代
值迭代算法计算一次。
策略迭代算法计算无限次迭代。
截断策略迭代算法计算有限次迭代(例如
伪代码:截断策略迭代算法
初始化:已知所有
的概率模型 和 。初始猜测 。 目标:搜索最优状态值和最优策略。
当
未收敛时,对于第 次迭代,执行以下操作: 策略评估:
初始化:选择初始猜测为。最大迭代次数设为 。 当
时,执行以下操作: 对于每个状态
,执行以下操作:
设置
策略改进:
对于每个状态
,执行以下操作: 对于每个动作
,执行以下操作:
- 计算
-值: - 计算最大动作值:
- 策略更新:如果
,则 ,否则
值迭代、策略迭代和截断策略迭代之间关系的示意图:
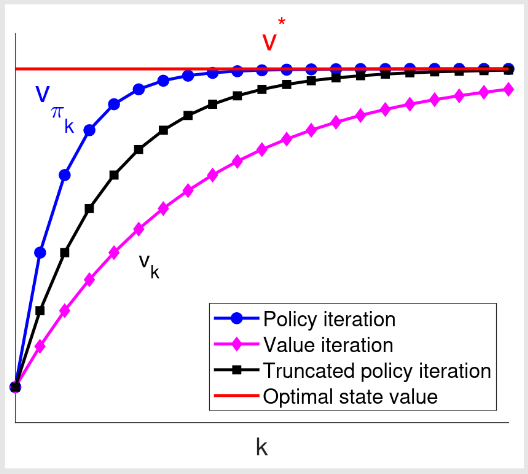
策略改进(PI)的收敛性证明基于值迭代(VI)的收敛性。由于 VI 收敛,可知 PI 也收敛。