PPO算法-chapter1-基础原理
PPO算法-chapter1-基础原理
Bohao Zhao[chapter-1]-基础原理
[PPO 算法]-强化学习基本概念
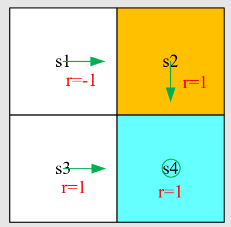
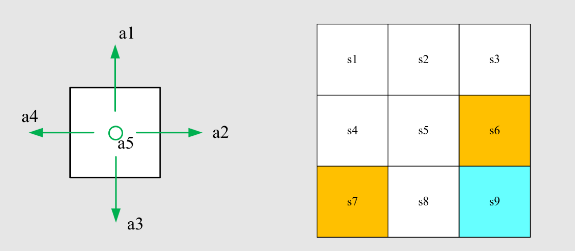
State:智能体相对于环境的状态,比如图中就有 9 个状态,每个状态可以是的向量组合
State space:状态的集合,一般数学上用花体来表示,表示形式为
Action:对于每一个状态的可能动作,比如图中左边智能体有五个选项,上下左右或不动
Action space:动作的集合,一般数学上用花体来表示,表示形式为
State transition:状态转移,从一个状态经过一个动作换到另外一个状态,可以表示为可以用表格来表示状态的转移情况:
State transition probability:状态转移概率,即用概率论来描述状态转移情况,如下式
代表智能体通过动作
从状态 转移到状态 的概率为 1;智能体通过动作 从状态状态 转移到状态 的概率为 0,即向右走不到非 的状态 Remark:此案例是确定性(deterministic)案例,真实的案例一般是随机的(stochastic)
Policy:策略,告诉 action 采用哪一个状态,如绿色箭头
策略用条件概率可以表述为
Remark:此案例是确定性(deterministic)案例,还有随机策略,如
策略可以用表格(编程时经常这么做)来呈现,如
Reward:奖励,是一个标量值,采取动作后获得的一个值;正数代表动作鼓励,负数代表动作的惩罚。例如边界惩罚:
,目标奖励 ,其他情况 Reward 可以理解为 Human-machine interface,即人机交互的一个接口,去引导智能体应该做什么和不应该做什么
Reward 表格直观表示
Reward 可以用数学方法来表示,比如如果在状态
采取行动 ,奖励 Reward = -1,则可以表示为
Trajectory:轨迹,是一个 state-action-reward 的一个链,可以用数学表示为:
Return:针对一个 Trajectory,是沿着这个 Trajectory 所有 Reward 的总和,量化地去评判哪一个策略比较好
Discounted return:和折扣因子(discount rate)结合使用,防止直接计算 Return 导致发散问题。如
Discounted return 可以使得 return 变得收敛,以及均衡更远未来和更近未来的奖励(
接近 0 倾向于更近未来-近视;接近 1 倾向更远未来-远视)
Episode:从开始状态,经过一个策略之后到达最终状态(terminal state)所形成的一个轨迹叫做 episode 或 trail一个 episode 通常是有限步的,这样的任务通常被称为 episodic tasks
有些任务是没有 terminal state 的,这样的任务我们称为 continuing tasks,一般描述任务可以是 episodic tasks 和 continuing tasks,但是可以将 episodic tasks 转换为 continuing tasks
转换方式 1:将目标 state 看成一个特殊的 absorbing state,即到达这个状态之后不论采取任何 action 他都会回到这个状态,或者直接让他在这个状态下的任何 action 的 reward=0
转换方式 2:将目标状态看成是一个普通状态带策略,如果策略好的话他就一直在这个状态,如果策略不好的话可能还会跳出来
MDP(Markov decision process) :马尔可夫决策过程,是个框架,包含很多要素,如
集合:
- 状态:状态的集合
- 动作:与状态
相关联的动作集合 - 奖励:奖励的集合
概率分布(或称为系统模型):
- 状态转移概率:在状态
下,采取动作 ,转移到状态 的概率是 - 奖励概率:在状态
下,采取动作 ,获得奖励 的概率是 - 策略:在状态
下,选择动作 的概率是 - 马尔可夫性质:无记忆性质
马尔可夫决策过程最重要的是其无记忆性质,其为后续的概率公式分析提供了很多便利性
如果 policy 一旦确定,那么马尔可夫决策过程就演变成了马尔可夫过程