PPO算法-chapter3-贝尔曼最优方程
PPO算法-chapter3-贝尔曼最优方程
Bohao Zhao[chapter-3]-贝尔曼最优方程
[PPO 算法]-最优策略和贝尔曼最优方程
前言
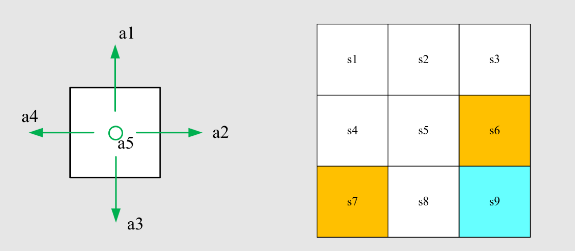
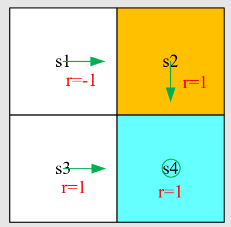
先介绍之前的例子

写出贝尔曼方程并求解状态值(设
求解线性方程组,得到 state-value:
计算状态
动作值:
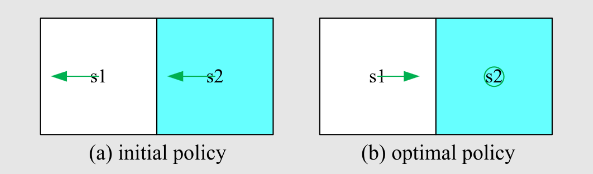
策略不好,我们如何改进它?可以根据动作值来改进策略。 特别是,当前策略
观察我们刚刚得到的动作值:
如果我们选择最大的动作值,那么,新策略是
这种新的好的策略如何去评估?如何迭代得到呢?后续介绍
[PPO 算法]-Optimal Policy
公式定义
状态值可以用来评估一个策略是否好:如果
那么
定义:如果
该定义引出许多问题:
- 最优策略是否存在?
- 最优策略是否唯一?
- 最优策略是随机的还是确定性的?
- 如何获得最优策略?
为了回答这些问题,下面介绍贝尔曼最优方程。先直接给出数学表达式-贝尔曼最优方程(元素形式):
注:
是已知的。 是未知的,需要计算。 是已知的还是未知的?是未知的,这就成为了一个优化问题
贝尔曼最优方程(矩阵-向量形式):
其中对应于
这里
$$ \max_{\pi} \begin{bmatrix}
- \ \vdots \
\end{bmatrix}
BOE 是巧妙而优雅的!为什么优雅?它以一种优雅的方式描述了最优策略和最优状态值。为什么复杂?右侧有一个最大化,可能不容易看出如何计算。
后续需要理解以下所有问题:
- 算法:如何解决这个方程?
- 存在性:这个方程有解吗?
- 唯一性:这个方程的解是唯一的吗?
- 最优性:它与最优策略有什么关系?
基本性质介绍
BOE:元素形式
BOE:矩阵-向量形式
上述矩阵向量形式具有未知量
思路:求解以下方程中的两个未知数
:
为了解这些方程,首先考虑右侧。无论
的值如何, ,其中最大化在 时达到。其次,当 时,方程变为 ,这使得 。因此, 和 是方程的解。
首先固定
假设
已知。找到 解决
其中
且 。 答案:假设
。那么,最优解是 和 。这是因为对于任何
受上述例子的启发,考虑到
其中最优性在以下情况下达到
其中
写成
先固定定
其中
这个方程看起来很简单。如何求解它?
一些概念
- 不动点:
是函数 的一个固定点,如果
- Contraction mapping(或收缩函数):
是一个Contraction mapping,如果
其中
必须严格小于 1,以便许多极限如 当 时成立。 - 这里
可以是任何向量范数
定理(压缩映射定理)
对于任何形式为
的方程,如果 是压缩映射,则:
- 存在性:存在一个不动点
满足 。 - 唯一性:不动点
是唯一的。 - 算法:考虑一个序列
,其中 ,则当 时, 。此外,收敛速度是指数级。
求解BOE
考虑到贝尔曼最优方程:
这个方程具有压缩性质,如下
定理(压缩性质)
是一个压缩映射,满足
其中
是折扣因子。
这里不过多介绍,可以进一步得到下面求解算法
定理(存在性、唯一性与算法)
对于BOE
,总是存在一个解 且该解是唯一的。该解可以通过迭代方法求解:
该序列
会以指数速度收敛到 ,给定任意初始猜测 。收敛速度由 决定。
假设
假设
那么
因此,
定理(策略最优性)
假设
是 的唯一解,并且 是满足 的状态值函数,对于任意给定的策略 ,则
根据这个定理这里就可以确定
最优策略
定理(贪心最优策略)
对于任意
,确定性贪心策略
是解决BOE的最优策略。这里,
其中
。
最优策略性质
哪些因素决定了最优状态值和最优策略?从BOE可以清楚地看到
有三个因素:
- 系统模型:
- 奖励设计:
- 折扣率:
其他是未知且待求解的
定理(最优策略不变性)
考虑一个马尔可夫决策过程,其中
是满足 的最优状态值。如果每个奖励 通过仿射变换 改变,其中 且 ,那么相应的最优状态值 也是 的仿射变换:
其中
是折扣率, 。因此,最优策略对奖励信号的仿射变换是不变的。