PPO算法-chapter9-演员评论家方法

[chapter-10]-Actor-Critic方法

[PPO算法]-演员评论家AC方法介绍

前言

Actor-Critic 方法仍属于策略梯度方法

  • 它们突出融合了策略梯度与基于价值方法的结构。

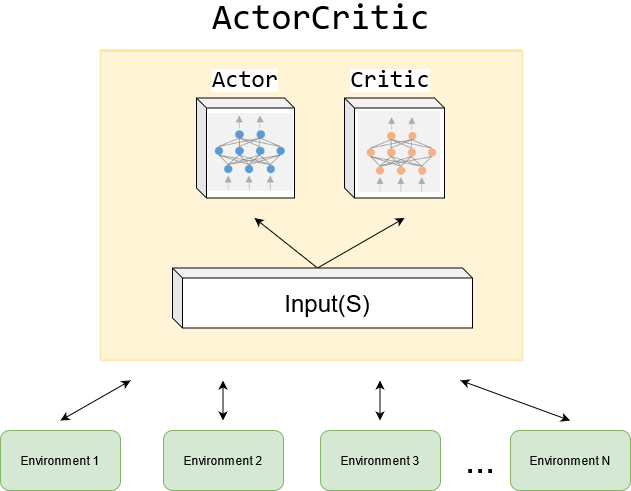
“Actor”与“Critic”分别指什么？

  • Actor：负责策略更新。因其策略将直接用于执行动作，故称“演员”。
  • Critic：负责策略评估或价值估计。因其通过评估来评判策略好坏，故称“评论家”。

最简单的AC

回顾上节课介绍的策略梯度思想

  1. 定义标量指标 ，可为 或 ：
  2. 最大化 的梯度上升算法：

  1. 随机梯度上升算法：

  • Actor：上述策略参数更新部分！
  • Critic：负责估计 的部分！

如何获得 ​ ？

目前，我们已学习两种估计动作价值的方法：

  • 蒙特卡洛（MC）学习：若使用 MC，对应算法称为 REINFORCE 或 蒙特卡洛策略梯度，上节课已介绍。
  • 时序差分（TD）学习：若使用 TD，这类算法通常称为 Actor-Critic，本节课将介绍。

最简单的 Actor-Critic 算法（QAC）

目标：通过最大化 寻找最优策略。

在每个回合的时间步 ​ ，执行：

  1. 依 生成 ，观测 ，再依 生成 。

  2. Critic（价值更新） ：

  3. Actor（策略更新） ：

备注：

  • Critic 对应“SARSA + 价值函数近似”。
  • Actor 对应策略更新算法。
  • 该算法为 on-policy（为何 PG 是 on-policy？）。
  • 由于策略是随机的，无需使用 -greedy 等技术。
  • 这种特定的 Actor-Critic 算法有时称为 Q Actor-Critic (QAC) 。
  • 尽管简单，它揭示了 Actor-Critic 方法的核心思想，后续可扩展出许多其他算法。

A2C方法

我们将 QAC 扩展为 优势演员-评论家（A2C）

  • 核心思想：引入Baseline以降低方差。

性质：策略梯度对附加基线不变：

其中附加基线 是仅依赖于状态 的标量函数。

接下来回答两个问题：

  • 为什么有效？
  • 为什么有用？

首先，为什么有效？

因为

详细推导：

第二，为什么基线有用？

梯度为

其中

  • 对 不变；
  • 对 并非不变。

原因：

而

若 过大（如 100 万）， 会很大，导致方差爆炸；合适的 可显著减小方差。

我们的目标：选择最优基线 以最小化

  • 好处：用随机样本近似 时，估计方差也会更小

在 REINFORCE 与 QAC 算法中

  • 没有使用基线
  • 或者说等价于设 ，但这未必是好的基线

最优基线：对于任意 ，最小化 的最优基线为

证明见教材。

尽管该基线最优，但形式复杂。可去掉权重 ，选择次优基线：

即状态 的状态价值！

当 时：

  • 梯度上升算法为

其中

称为优势函数（为何叫“优势”？）。

  • 该算法的随机版本为

进一步，算法可重写为

  • 步长与相对价值 成正比，而非绝对价值 ，更加合理。
  • 仍能很好地平衡探索与利用。

优势演员-评论家（A2C）或称 TD 演员-评论家

目标：通过最大化 寻找最优策略。

每个回合的时间步 ​ ，执行：

  1. 依策略 生成动作 ，观测 。

  2. TD 误差（优势函数） ：

  3. Critic（价值更新） ：

  4. Actor（策略更新） ：

算法为 on-policy；因策略 随机，无需 -greedy 等技巧。

Off-policy的AC

策略梯度是 on-policy 的

  • 原因：梯度为 ，必须从当前策略 采样。

能否转为 off-policy？

  • 可以，通过重要性采样。
  • 重要性采样不仅适用于 AC，也适用于任何需要估计期望的算法。

考虑随机变量 。
若其概率分布为 ：

则期望为

问题：如何利用样本 估计 ？

情况 1（我们已熟悉） ：

  • 样本 按照 生成：

  • 则样本均值收敛于期望：

    当

因为

详见大数定律。

情况 2（我们要研究的新情况） ：

  • 样本 按照另一分布 生成：

  • 其期望为

  • 若直接使用样本均值，则显然

问题：能否用 来估计 ？

  • 为何要这样做？
    我们可能希望基于行为策略 的样本，估计目标策略 下的期望 。

  • 如何做？

    • 若直接使用样本均值，会收敛到 ，无法达成目标。
    • 可通过重要性采样技术实现。

注意到

因此，可通过估计 来估计 。

如何估计 ​ ？ 简单，令

则：

问题： 可能会问：虽然 需要 ，若已知 ，为何不直接计算期望？

回答：适用于：

  • 仅在给定 时易计算 ，但期望难以计算时适用。
  • 例如，连续情况复杂 ，或 无表达式（如 由神经网络表示）。

与之前 on-policy 情况类似，我们需要推导 off-policy 下的策略梯度。

  • 假设 是生成经验样本的行为策略。
  • 目标是利用这些样本更新目标策略 以最小化指标

其中 是 下的平稳分布。

定理（离策略梯度定理）

在折扣因子 的折扣情况下， 的梯度为

其中 是行为策略， 是状态分布。

离策略梯度对基线 也不变。

  • 特别地，有

  • 为降低估计方差，可选基线 ，得

对应的随机梯度上升算法为

与 on-policy 类似地，

则算法变为

因此

DPG

截至目前，策略梯度方法中使用的策略都是随机的，因为对于每个 ，都有 。
我们能否在策略梯度方法中使用确定性策略？

  • 优点：它可以处理连续动作。

策略的表示方法

  • 到目前为止，一般策略表示为 ，可以是随机的，也可以是确定性的。

  • 现在，确定性策略特别表示为

  • 是从状态空间 到动作空间 的映射。

  • 可以用例如神经网络表示，输入为 ，输出为 ，参数为 。

  • 我们可以简写 为 。

考虑在折扣情形下的平均状态价值指标：

其中， 是一个概率分布，满足 。

  • 被选择与 无关。在这种情况下，梯度更容易计算。

有两种特殊但重要的选择 的情况：

  • 第一种特殊情况是： 且 ，其中 是一个特定的起始状态。
  • 第二种特殊情况是： 是一个不同于 的行为策略的平稳分布。

定理（折扣情形下确定性策略梯度定理）

在折扣情形中，其中 ， 的梯度为：

其中， 是一个状态分布。

确定性Actor-Critic算法

初始化：

  • 给定行为策略
  • 确定性目标策略 ，其中 为初始参数向量
  • 值函数 ，其中 为初始参数向量

目标：通过最大化 搜索最优策略

在每个时间步 的回合中执行：

  • 根据 生成动作 ，并观测

TD误差：

Critic（值函数更新）：

Actor（策略更新）：

备注：

  • 这是一个离策略实现，其中行为策略 可以与 不同。

  • 也可以被替换为 。

  • 如何选择用于表示 的函数？

    • 线性函数：，其中 是特征向量。细节可参考 DPG 论文。
    • 神经网络：深度确定性策略梯度（DDPG）方法。

​

‍