粒子群算法
粒子群算法
Bohao Zhao粒子群算法学习
简介~
==因鸟而起~==:
- 1995年,美国社会心理学者James Kennedy和电气工程师Russell Eberhart合作提出了粒子群算法。他们在模拟鸟群觅食的社会模型时获得了启发,将这个模型应用到优化问题求解中,开发出了粒子群算法。
- 该算法模拟鸟群觅食的行为,每个解对应一个鸟,称为“粒子”。粒子在解空间飞行,当粒子发现更好的解时,会向那里飞行。全体粒子最终会聚集到最优解处。
- 粒子群算法借鉴了遗传算法的思想,但它没有遗传算法的选育、交叉、变异等操作。其只根据粒子本身经验和群体经验来调整粒子的飞翔方向和速度。
- 与遗传算法等其他群智能优化算法相比,粒子群算法具有计算简单、易实现、快速收敛等特点,因此应用广泛。
粒子群优化~
工作原理
假设有一群鸟在某个区域觅食,目标是找到食物最丰富的地方。
- 每只鸟可以看作一个“粒子“,它可以在区域内飞翔,代表算法中的一个潜在解。
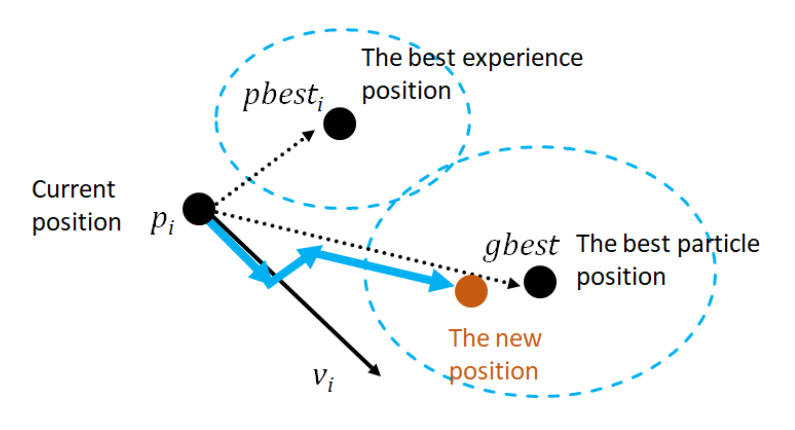
- 每只鸟有一个当前位置(解)和飞翔速度。它会根据自身以往的觅食经验,和群体中其他鸟所传递的食物信息,来调整自己的飞行方向和速度。
- 每只鸟都记载着它自己发现过的食物最丰富的位置(个体经验最优,pbest)。整群鸟发现的食物最丰富区域就是全局最优(gbest)。
- 随着时间的迭代,每只鸟根据下式更新自己的速度和位置: 新速度 = 旧速度 + 自身经验 + 群体经验 新位置 = 旧位置 + 新速度
- 自身经验是它飞向自己最佳地点的趋势,群体经验是它飞向群体最佳地点的趋势。
- 通过这个更新过程,整群鸟会最终聚集在食物最多的那片区域。
基本参数
表示一大群粒子集合 表示群体中具有位置 和速度 的个体 为粒子 的位置 为粒子在 位置的速度 为单个粒子的最优解(经验) 为粒子群的最优解(经验),也就是全局最优解 为适应度函数 为加速度函数(认知和社会参数) 为介于0~1之间的随机数 为迭代次数
迭代方程
式(1)为速度更新方程,式(2)为位置更新方程。
上一次迭代的速度; 代表粒子本身经验的影响, 为粒子本身经验对自身的置信度, 为自身经验影响的随机效应; 代表社会经验对粒子的影响, 为社会经验对自身的置信度, 为社会经验影响的随机效应; - 根据新得到的速度
来更新位置 ; 为对上一次动作的信任程度,一种自适应调整的策略,随着迭代次数的增加,惯性权重 不断减小,从而使得粒子群算法在初期具有较强的全局收敛能力,在后期具有较强的局部收敛能力;
粒子当前位置
的个体经验会驱使它走向 处,但是收到群体经验的影响粒子也会趋向 处,根据其他因素 的影响粒子同时会进行方向折中(两个方向都沾点)和幅度折中(两个方向的比例都沾点),根据式(1)可以得出最后的速度,从而驱动粒子从当前位置 走向新的位置,从而完成迭代。
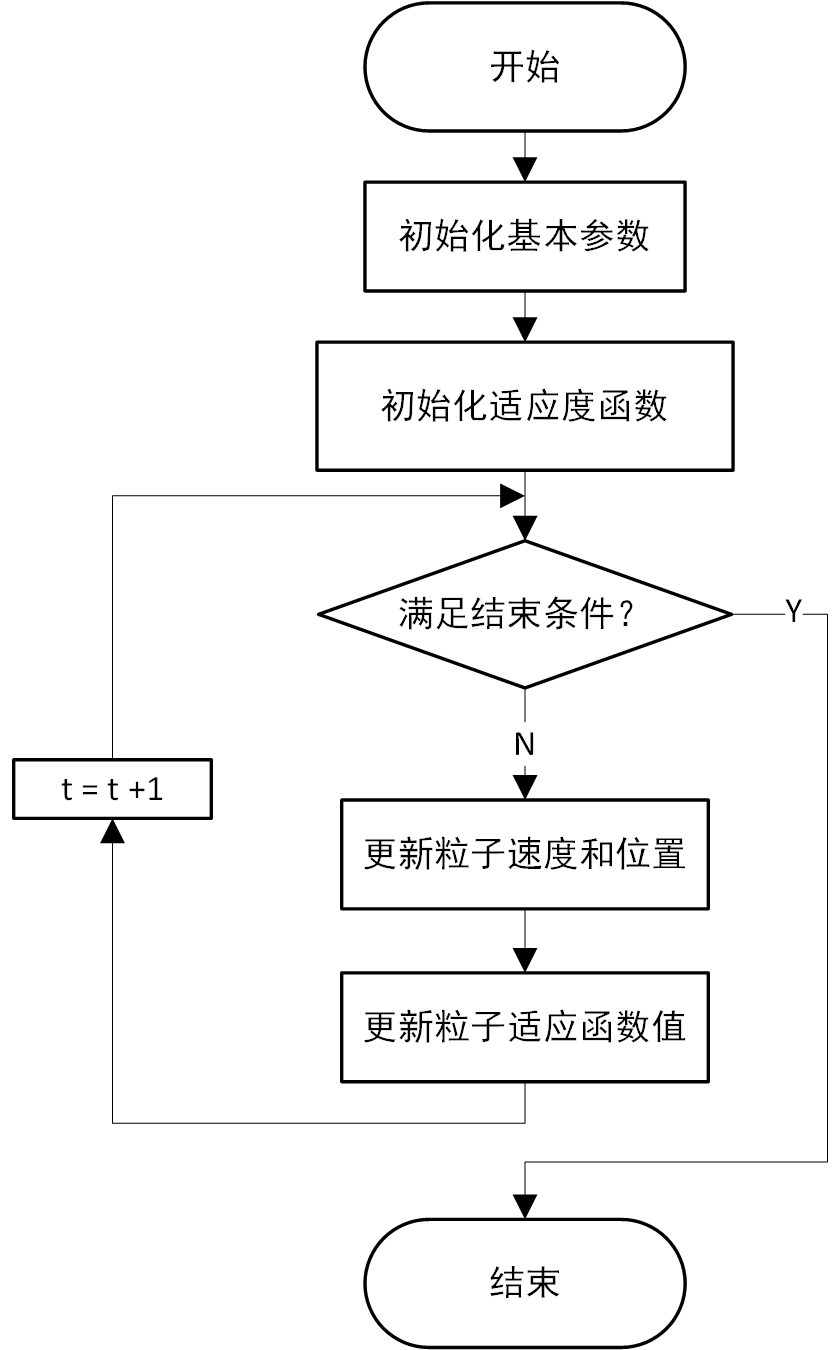
优化步骤
优化举例~
问题描述
Example:
已知函数
其中 求解y的最小值
Matlab代码
1 | clc;clear;close all; |
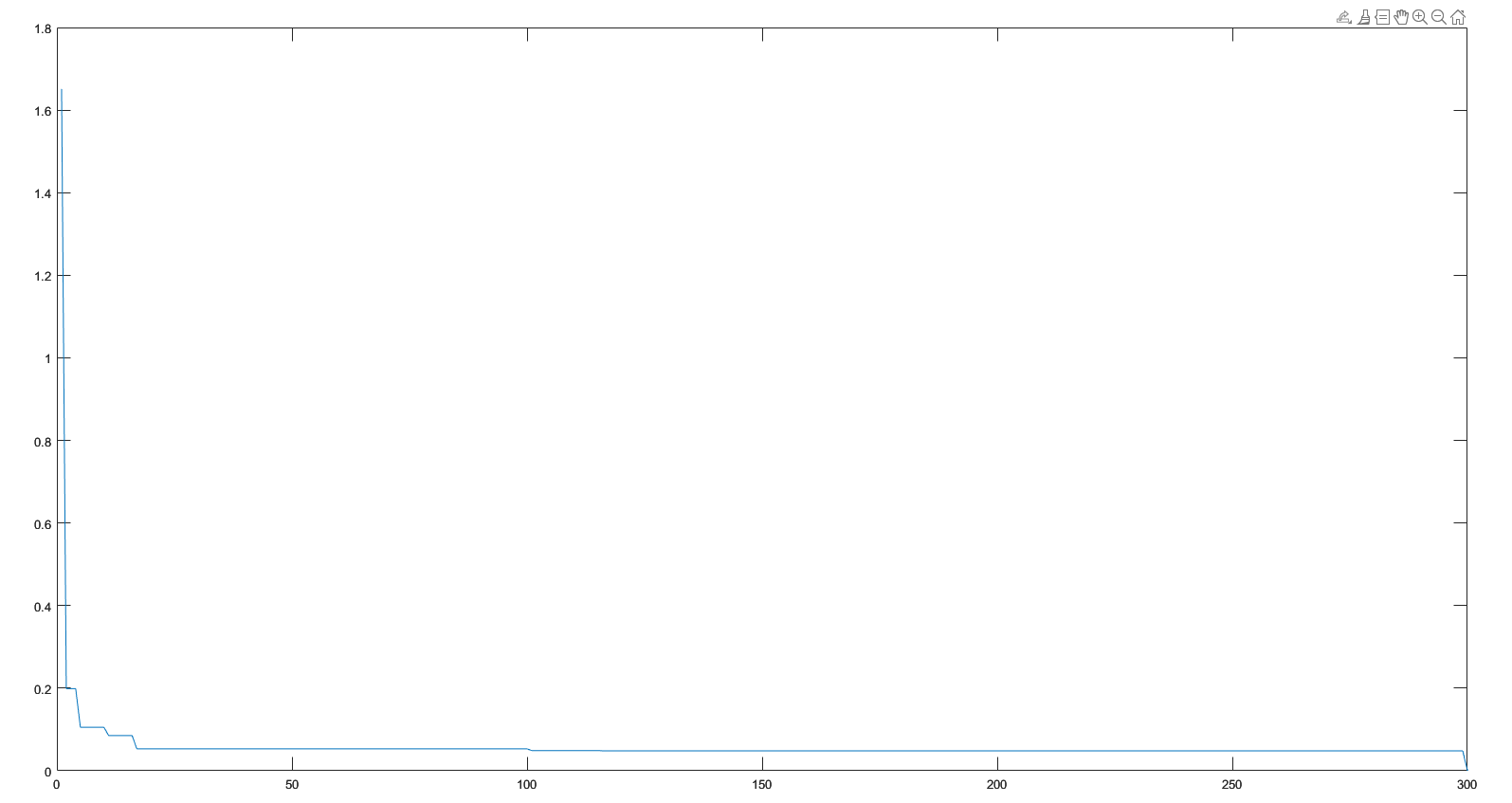
仿真结果
结果显示其找到了接近全局最小0的解,但是未收敛到0处
Reference:
[1] 粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读 - 知乎 (zhihu.com)
评论
匿名评论隐私政策
✅ 你无需删除空行,直接评论以获取最佳展示效果