PPO算法-chapter2-贝尔曼方程
PPO算法-chapter2-贝尔曼方程
Bohao Zhao[chapter-2]-贝尔曼方程
[PPO 算法]-贝尔曼方程
前言
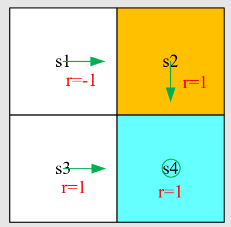
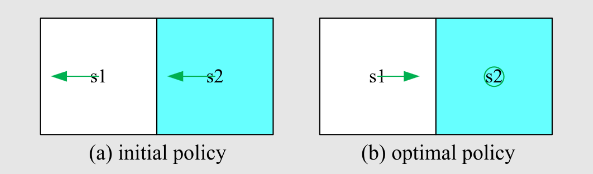
return 是非常重要的，可以去评估策略，是建立起数学和直观感觉的纽带，先看例子：
哪一个策略最好，哪个策略最差？
可以用数学去表达，即用计算 return 来评估 return（注意一般所说的 return 指的是 discounted return，涉及到无穷级数求和数学知识）
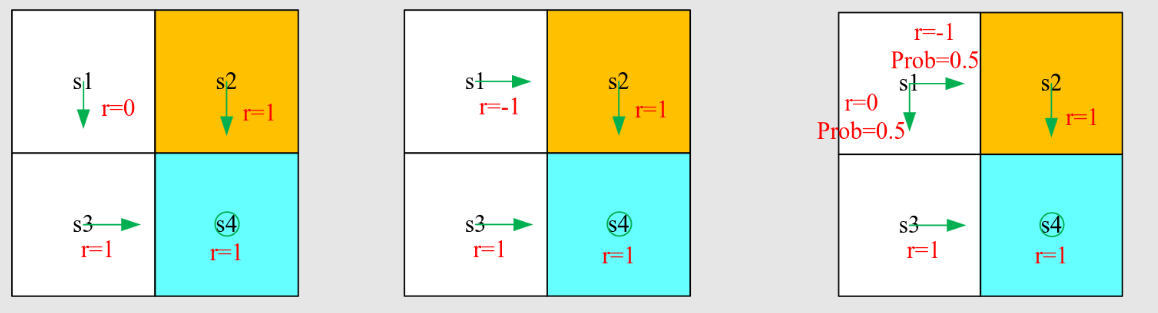
注意这里只计算第三个轨迹的 return 为例，因为其是随机的：
如何去计算reward？对于下面的轨迹来说：
方法1：设
方法2(Bootstrapping)：
这种方法叫做自举，从自己出发得到自己，类似于递归
用矩阵来表示为：
可以简写为：
这就是确定性策略的贝尔曼公式，可以用线性代数求解此线性方程组
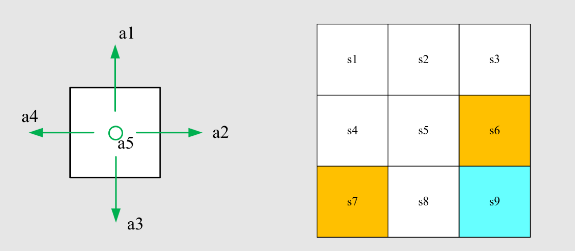
State Value
考虑以下单步过程：
：离散时间实例 ：时间 的状态 ：在状态 采取的动作 ：采取 后获得的奖励 ：采取 后转换到的状态
注意
这一步由以下概率分布控制：
由 得到 由 得到 由 得到
目前，我们假设我们知道模型（即概率分布）
考虑以下多步轨迹：
折扣回报为
是折扣率。 也是一个随机变量，因为 是随机变量。
定义
注：
- 它是
的函数。它是在状态从 开始的条件下的条件期望。 - 它基于策略
。对于不同的策略，状态值可能不同。
return和state-value之间的关系是什么？
state-value是从状态开始可以获得的所有可能回报的平均值。如果所有
现在再看前言的三个策略，计算他们的state-value：
可知策略
贝尔曼公式
描述了所有状态值之间的关系
简单来说，贝尔曼公式描述了所有state-value直接的关系
考虑一个随机轨迹：
回报
然后，根据状态值的定义，有
接下来，分别计算这两个项。
首先，计算第一项
这是瞬时奖励的期望
接着，计算第二项
这是未来奖励的均值
由于无记忆的马尔可夫性质。
因此，我们有
此方程中的符号
和 是要计算的状态值。自举法！ 是给定的策略。解这个方程称为策略评估。 和 表示动态模型。如果模型是已知或未知的呢？
注意：
上述方程称为贝尔曼方程，它描述了不同状态的状态值函数之间的关系。
它由两项组成：即时奖励项和未来奖励项。
一组方程：每个状态都有一个这样的方程！
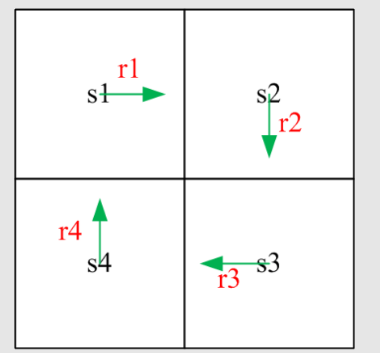
如何理解贝尔曼方程？考虑例子：
根据一般表达式写出贝尔曼方程：
这个例子很简单，因为策略是确定性的
首先，考虑状态值
且 。 且 。 且 。
将它们代入贝尔曼方程得到
同样，可以得到
解上述方程，从最后一个到第一个：
如果
计算完状态值后我们该怎么办？要有耐心（计算动作值并改进策略）
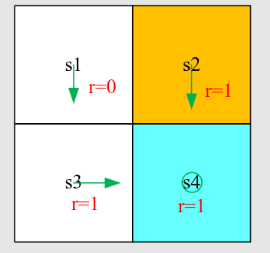
例2：
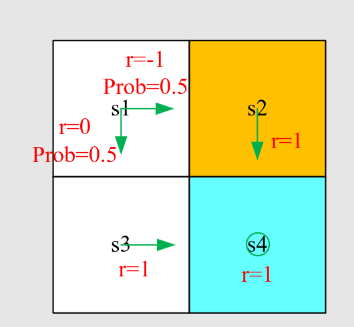
答案：
$$ v_{\pi}(s_1) = 0.5[0 + \gamma v_{\pi}(s_3)] + 0.5[-1 + \gamma v_{\pi}(s_2)]\
v_{\pi}(s_2) = 1 + \gamma v_{\pi}(s_4)\
v_{\pi}(s_3) = 1 + \gamma v_{\pi}(s_4)\
v_{\pi}(s_4) = 1 + \gamma v_{\pi}(s_4)\ $$
解上述方程，从最后一个到第一个。
将
与之前的策略比较。这个更差。
贝尔曼公式矩阵和向量形式
为什么考虑矩阵-向量形式？因为我们需要从中求解state-value
一个未知数依赖于另一个未知数。如何解决这些未知数？
元素形式：上述元素形式对每个状态
矩阵-向量形式：如果我们把所有方程放在一起，我们有一组线性方程，可以简洁地写成矩阵-向量形式。矩阵-向量形式非常优雅且重要。
回顾：
将贝尔曼方程重写为
其中
假设状态可以被索引为
将所有状态的这些方程放在一起并重写为矩阵-向量形式
其中
，其中 ，是状态转移矩阵
如果有四个状态，
$$
例1：
.zip.af3/[强化学习]-PPO算法/assets/image-20250904105507-q55svo3.png)
其贝尔曼方程可以表示为
$$
例2：
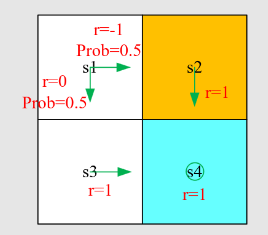
其贝尔曼方程可以表示为
$$
为什么要解state-value？
- 给定一个策略，找出对应的状态值称为策略评估（Policy Evaluation）
- 这是强化学习（RL）中的一个基本问题。它是找到更好策略的基础。
- 因此，理解如何解贝尔曼方程是很重要的。
贝尔曼方程的矩阵-向量形式是
（1）闭式解是：
- 矩阵
是可逆的。 - 我们仍然需要使用数值算法来计算矩阵的逆。
- 可以避免矩阵求逆操作吗？可以
（2）一种迭代解是：
该算法导致一个序列
证明过程略
Action Value
从state value到action value：
- state value：智能体从某个状态开始可以得到的平均回报。
- action value：智能体从某个状态开始并采取某个动作可以得到的平均回报。
为什么我们关心动作值？因为我们想知道哪个动作更好。
定义：
是状态-动作对 的函数 依赖于
根据条件期望的性质，可以得出（类似全概率公式）
因此，
此外，回忆一下状态值由以下公式给出
我们得到动作值函数为
状态值公式揭示了如何从动作值得到状态值，动作值函数揭示了如何从状态值得到动作值
例：
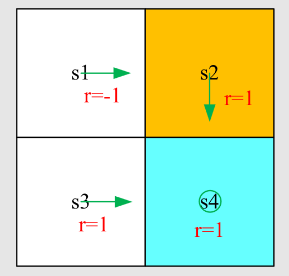
写出状态
问题：
不一定为0！
