等价输入干扰：Matlab求解LMI

等价输入干扰EID：Matlab求解LMI

镇稳目标

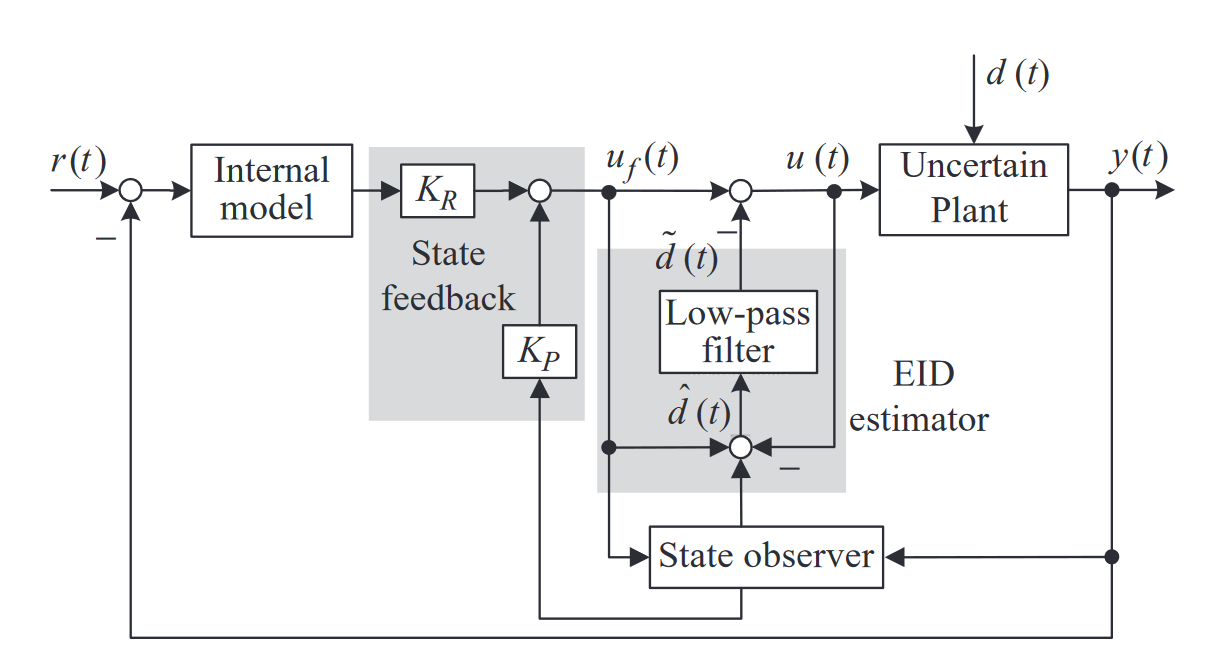
使EID系统镇稳的LMI推导详细请见上篇。

本篇论文中，使整个系统稳定的LMI条件为：

待定LMI变量为，其中前四个为对称半正定矩阵，后三个为合适矩阵即可

(1)式和(2)式内各参数为：

求解后可得参数：

基于 Yalmip 的 Matlab 程序编写

初始化准备

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
%清空环境
clear;  clc;

%系统矩阵
A = [-2 3; 4 -5];
B = [1;1]; 
C = [2 1];
Bd = [2;1];
M = [-1;0];

%系统参数
AF = -101;  
BF = 100;
CF = 1; 

%计算伪逆BZ
BZ = pinv(B);

%svd分解
[U,S,V] = svd(C);
V1 = V(:,1);
V2 = V(:,2);
S = S(1); 

%权重，不晓得干嘛的
w = 0.5;

%其他参数
a=1;
b=1;
alfa_1 = 1;
alfa_2 = 1;

定义sdpvar变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
% 半正定矩阵变量X
X1 = sdpvar(2);
X11 = sdpvar(1);
X22 = sdpvar(1);
X3 = sdpvar(1);
X4 = sdpvar(1);

%X2表达式
%V1*X11*V1'+V2*X22*V2'
X2=V1*X11*V1'+V2*X22*V2';

% 合适矩阵变量W
W1 = sdpvar(1,2);
W2 = sdpvar(2,1);
W3 = sdpvar(1);

构建LMI不等式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
%不等式1
pusai_11 = (A*X1+alfa_1*X1)+(A*X1+alfa_2*X1)'+B*W1+(B*W1)';
pusai_12 = W2*C+B*M'*X2;
pusai_13 = W2*C*M+B*X3;
pusai_14 = 0*ones(size(pusai_13));%适当维度的全零矩阵
pusai_22 = (A*X2+alfa_2*X2)+(A*X2+alfa_2*X2)'-W2*C-(W2*C)'-B*M'*X2-(B*M'*X2)';
pusai_23 = -B*X3+C'*W3'+A*X2*M+alfa_2*X2*M-W2*C*M;
pusai_24 = -B*CF*X4+(BF*BZ*W2*C)'+X2*M*BF;
pusai_33 = W3*C*M+(W3*C*M)';
pusai_34 = X3*BF'+(BF*BZ*W2*C*M)';
pusai_44 = (AF+BF*CF)*X4+((AF+BF*CF)*X4)';

eq1 = [pusai_11  pusai_12  pusai_13  pusai_14;
       pusai_12' pusai_22  pusai_23  pusai_24;
       pusai_13' pusai_23' pusai_33  pusai_34;
       pusai_14' pusai_24' pusai_34' pusai_44;
      ];

%不等式2
Z_22 = zeros(size(X1));          %2*2全零矩阵
Z_21 = [0;0];
eq2 = [X1    Z_22    Z_21  Z_21;
       Z_22' X2      X2*M  Z_21;
       Z_21' (X2*M)' X3    0;
       Z_21' Z_21'   0     X4;
      ]

注意上式的全零阵的维度，也就是观察整个矩阵保持方阵的维度正确

LMI约束编程

1
2
3
4
5
6
7
8
% LMI约束
F = [X1 >= 0];
F = F + [X11 >= 0];
F = F + [X22 >= 0];
F = F + [X3 >= 0];
F = F + [X4 >= 0];
F = F + [eq1 <= 0];
F = F + [eq2 >= 0];

求解LMI

1
2
3
4
5
6
7
8
9
% 求解LMI 
sol = optimize(F);
if sol.problem == 0
    disp("求解成功");
elseif sol.problem == 1
        disp( "求解失败，无可行解");
    else
        disp( "求解失败，其他错误");
end

提取解

1
2
3
4
5
6
7
8
9
% 提取解
X1 = value(X1);
X11 = value(X11);
X22 = value(X22);
X3 = value(X3);
X4 = value(X4);
W1 = value(W1);
W2 = value(W2);
W3 = value(W3);

这里我都提取了，其实只需要些许解就ok了，不过无伤大雅

7.计算反馈控制器

1
2
3
4
5
6
% 计算反馈控制器
L1 = W2*U*S*inv(X11)*inv(S)*U'
L2 = W3*U*S*inv(X11)*inv(S)*U'
L3 = BZ*L1
Kp = W1*inv(X1)
B1=BZ;

C.仿真实战

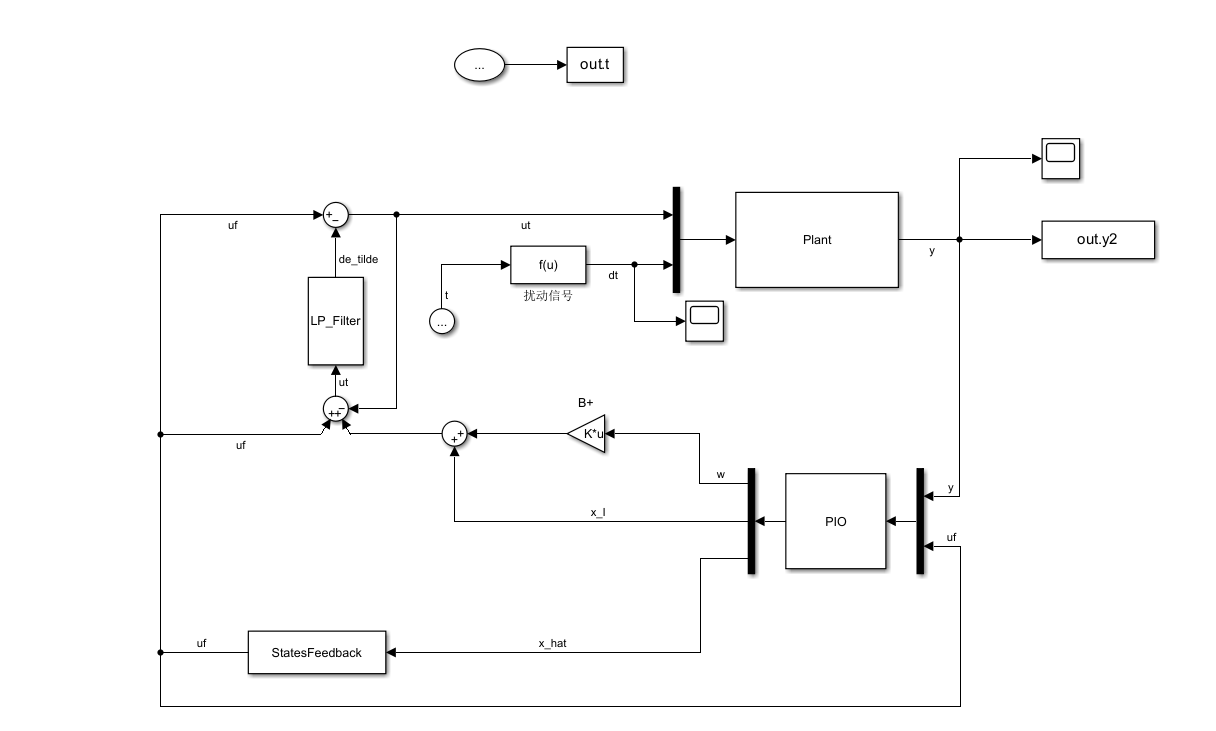
仿真模型（s-function搭建）

在这里插入图片描述

干扰信号图

在这里插入图片描述

论文中LMI解得参数抑制后的输出效果

在这里插入图片描述

本文yalmip工具解得参数抑制输出效果

在这里插入图片描述

结论：用另外一种LMI工具一样可以解出可行参数使系统达到镇定效果

参考文献

[1] M. Wu, F. Gao, P. Yu, J. She, and W. Cao, “Improve Disturbance-Rejection Performance for an Equivalent-Input-Disturbance-Based Control System by Incorporating a Proportional-Integral Observer,” IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, vol. 67, no. 2, 2020, doi: 10.1109/TIE.2019.2898627.