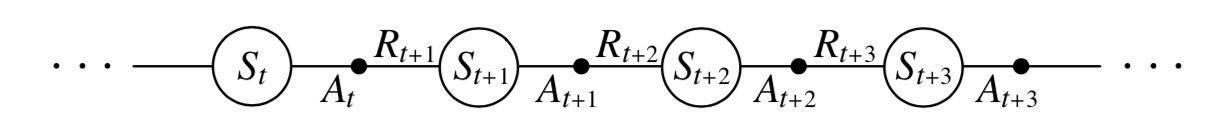[chapter-3]-贝尔曼最优方程
[PPO
算法]-最优策略和贝尔曼最优方程
前言
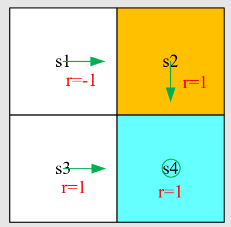
先介绍之前的例子
写出贝尔曼方程并求解状态值(设 ),贝尔曼方程:
求解线性方程组,得到 state-value:
计算状态
的五个动作的动作值
动作值:
策略不好,我们如何改进它?可以根据动作值来改进策略。 特别是,当前策略
是
观察我们刚刚得到的动作值:
如果我们选择最大的动作值,那么,新策略是
这种新的好的策略如何去评估?如何迭代得到呢?后续介绍
[PPO 算法]-Optimal Policy
公式定义
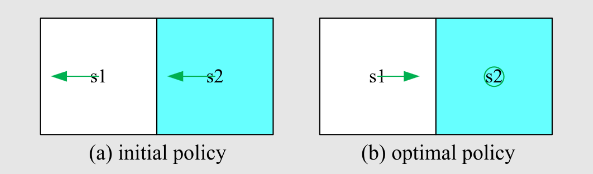
状态值可以用来评估一个策略是否好:如果
那么 比 更“好”
定义:如果 对于所有
和任何其他策略 ,那么说这个策略
是最优的,
该定义引出许多问题:
最优策略是否存在?
最优策略是否唯一?
最优策略是随机的还是确定性的?
如何获得最优策略?
为了回答这些问题,下面介绍贝尔曼最优方程。先直接给出数学表达式-贝尔曼最优方程(元素形式):
注:
是已知的。
是未知的,需 ...
[chapter-1]-基础原理
[PPO 算法]-强化学习基本概念
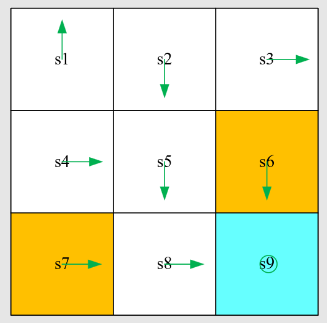
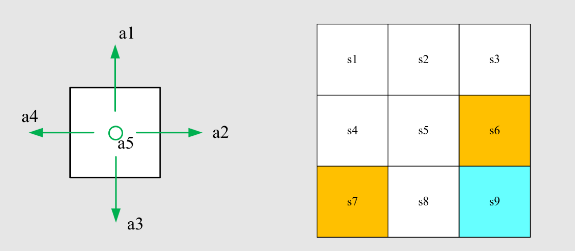
State:智能体相对于环境的状态,比如图中就有
9 个状态,每个状态可以是
的向量组合
State space:状态的集合,一般数学上用花体来表示,表示形式为
Action:对于每一个状态的可能动作,比如图中左边智能体有五个选项,上下左右或不动
Action space:动作的集合,一般数学上用花体来表示,表示形式为
State transition:状态转移,从一个状态经过一个动作换到另外一个状态,可以表示为
可以用表格来表示状态的转移情况:
State transition probability:状态转移概率,即用概率论来描述状态转移情况,如下式
代表智能体通过动作 从状态
转移到状态 的概率为 1;智能体通过动作 从状态状态 转移到状态 的概率为 0,即向右走不到非
的状态
Remark:此案例是确定性(deterministic)案例,真实的案例一般是随机的(stochastic)
...
[chapter-8]-值函数近似
[PPO算法]-值函数近似和DQN
前言
迄今为止,本书中状态值与动作值均用表格表示。
例如,动作值:
例如,状态值:
状态
值
优点:直观且易于分析。
缺点:难以处理大规模或连续的状态或动作空间,主要体现在两个方面:
存储:表格大小随状态/动作数量线性增长,内存开销大;
泛化能力:无法对未见过的状态或动作进行合理估值。
考虑一个例子:
有 个状态:。
这些状态在策略 下的值为
。
非常大!
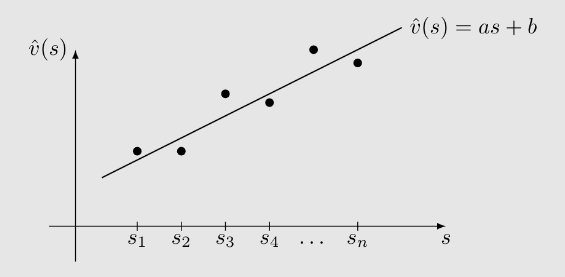
我们希望用一条简单的曲线来近似这些值。
例如,可以使用支线来拟合这些点:
设这条直线的方程为
其中
为参数向量;
为状态
的特征向量;
对 是线性 ...
[chapter-10]-Actor-Critic方法
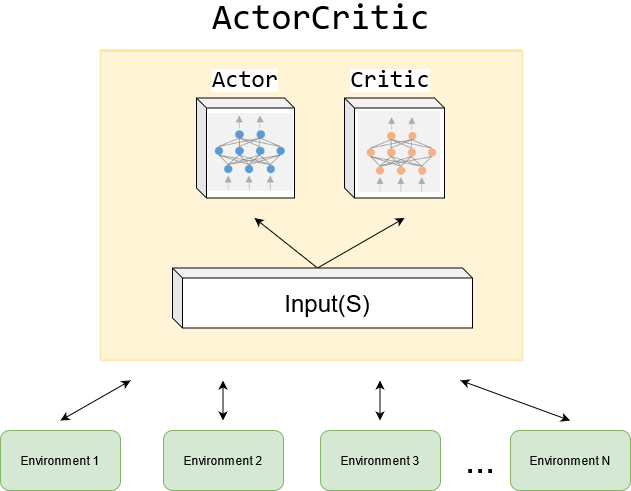
[PPO算法]-演员评论家AC方法介绍
前言
Actor-Critic 方法仍属于策略梯度方法
它们突出融合了策略梯度与基于价值方法的结构。
“Actor”与“Critic”分别指什么?
Actor:负责策略更新。因其策略将直接用于执行动作,故称“演员”。
Critic:负责策略评估或价值估计。因其通过评估来评判策略好坏,故称“评论家”。
最简单的AC
回顾上节课介绍的策略梯度思想
定义标量指标 ,可为
或 :
最大化
的梯度上升算法:
随机梯度上升算法:
Actor:上述策略参数更新部分!
Critic:负责估计 的部分!
如何获得
?
目前,我们已学习两种估计动作价值的方法:
蒙特卡洛(MC)学习:若使用 MC,对应算法称为
REINFORCE 或
蒙特卡洛策略梯度,上节课已介绍。
时序差分(TD)学习:若使用 TD,这类算法通常称为
Actor-Critic,本节课将介绍。
最简单的 Actor-C ...
[chapter-4]-值迭代和策略迭代
[PPO
算法]-基于模型的算法-值迭代和策略迭代
值迭代(Value Iteration)
如何解决贝尔曼最优方程?
压缩映射定理提出了一种迭代算法:
其中
可以是任意的。这个算法最终可以找到最优状态值和最优策略。这种算法称为值迭代
接下来研究这种算法的实现,其可以分解为两个步骤。
步骤1:策略更新。这一步是求解
其中 是给定的。
步骤2:值更新。
问题:
是状态值吗?不是,因为不能确保
满足贝尔曼方程。
策略更新
逐元素形式的
是
解决上述优化问题的最优策略是
其中 。
被称为贪心策略,因为它简单地选择最大的 -值。
值更新
逐元素形式的
是
由于
是贪婪的,上述方程简化为
根据上面的步骤,可以得到如下的伪代码
伪代码:值迭代算法
初始化:已知所有
的概率模型 和 。初始猜测 。
目标:搜索解决贝尔曼最优方程的最优状态值和最优策略。
当 未收敛,即
大于预定义的小阈值时,对于第
次迭代,执行以下 ...
[chapter-7]-时序差分算法
需要注意的是 ,其中上标仅表示 的不同分解结构
[PPO算法]-TD-时序差分算法
前言
我们接下来考虑一些随机问题,并展示如何使用 RM 算法来解决它们。
首先,重新审视均值估计问题:基于一些独立同分布样本 计算
我们上节课已经研究过这个问题。
通过写出 ,我们可以将问题重新表述为一个求根问题
由于我们只能获得 的样本 ,噪声观测值为
根据上节课的内容,我们知道解决 的 RM 算法是
其次,考虑一个稍微复杂的问题。即基于 的一些独立同分布样本 来估计函数 的均值,
为了解决这个问题,我们定义
然后,问题变为一个求根问题:。相应的 RM 算法是
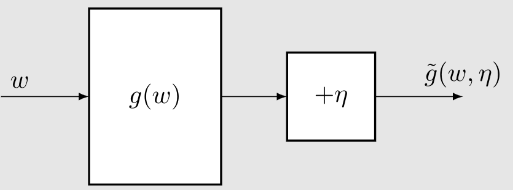
第三,考虑一个更复杂的问题:计算
其中 是随机变量, 是常数, 是一个函数。
假设我们可以获得 和 的样本 和 。我们定义
然后,问题变为一个求根问题:。相应的 RM 算法是
这个算法看起来像后面展示的 TD 算法。
TD之状态值
...
[chapter-9]-策略梯度方法
[PPO算法]-策略梯度-梯度上升和Reinfore
前言
此前,策略一直以表格形式表示:
所有状态的动作概率存储在一张表
中,表的每个条目由状态-动作对索引。
现在,策略也可以用带参数的函数表示:
其中
是参数向量。
该函数可以是神经网络,输入为状态 ,输出为执行每个动作的概率,参数为 。
优点:当状态空间很大时,表格表示在存储和泛化方面效率低下。
函数表示有时也写作 、
或 。
表格表示与函数表示的差异:
首先,如何定义最优策略?
在表格情形中,策略
最优当且仅当它能最大化每个状态的价值。
在函数情形中,策略
最优当且仅当它能最大化某个标量指标。
其次,如何获取某个动作的概率?
在表格情形中,可直接查表获得在状态 下采取动作 的概率。
在函数情形中,需根据函数结构与 ...
[chapter-5]-蒙特卡洛方法
[PPO
算法]-一种model-free的方法-蒙特卡洛方法
前言
老规矩,先给出一个示例:抛硬币问题
结果(正面或反面)表示为随机变量 :
如果结果是正面,则
如果结果是反面,则
目标是计算 。
方法1:使用模型
假设已知概率模型为
根据定义
问题:可能无法知道精确的分布!
方法2:无模型或称为模型无关
想法:多次抛硬币,然后计算结果的平均值。
假设我们得到一个样本序列:。那么均值可以近似为
这就是蒙特卡洛估计的思想!
数学依据
大数定律
对于一个随机变量 ,假设
是一些独立同分布(iid)样本。令 为样本的平均值。那么,
因此, 是 的无偏估计,并且其方差随着
增加到无穷大而趋近于零。
MC算法介绍
回顾策略迭代步骤
策略迭代在每次迭代中有两个步骤:
策略评估:
策略改进:
策略改进步骤的逐元素形式是:
关键是计算
从model-based到model-free
两种动作值的表达式:
...
[chapter-6]-随机近似理论和随机梯度下降
[PPO算法]-随机近似和随机梯度下降
前言
重新审视均值估计问题:
考虑一个随机变量 。
假设我们收集了一组独立同分布样本 。
我们的目标是估计 。
的期望可以通过以下方式近似
这种近似是蒙特卡洛估计的基本思想。
我们知道 当 。
为什么我们如此关心均值估计?
强化学习中的许多量如动作值和梯度都是定义为期望值!
新问题:如何计算均值 ?
我们有两种方法。
第一种方法是收集所有样本然后计算平均值。
这种方法的缺点是,如果样本是逐个收集的,我们必须等待所有样本收集完毕。
第二种方法可以避免这种缺点,因为它以增量和迭代的方式计算平均值。
特别地,假设
因此
那么 可以用 表示为
因此,我们得到以下迭代算法:
验证:我们可以使用
来递增计算均值 :
关于该算法的说明:
该算法的优势是增量的。一旦收到样本,即可立即获得均值估计。然后,均值估计可以立即用于其他目的。
由于样本不足,开始时均值估计不准确( ...
[chapter-2]-贝尔曼方程
[PPO 算法]-贝尔曼方程
前言
return
是非常重要的,可以去评估策略,是建立起数学和直观感觉的纽带,先看例子:
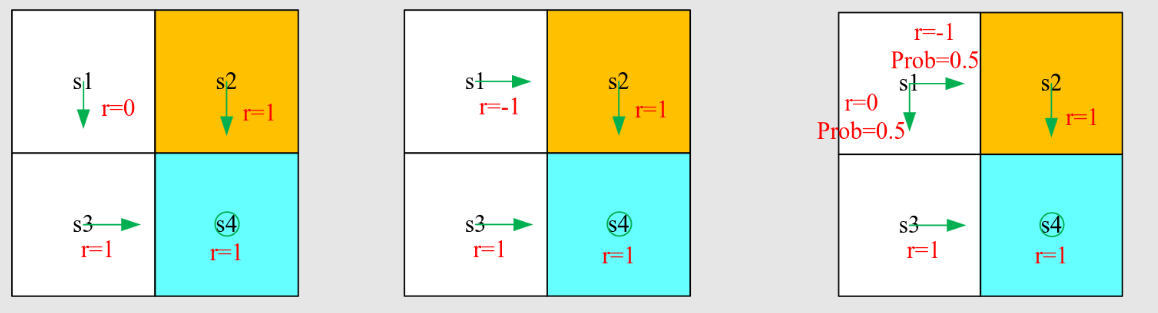
哪一个策略最好,哪个策略最差?
可以用数学去表达,即用计算 return 来评估 return(注意一般所说的
return 指的是 discounted return,涉及到无穷级数求和数学知识)
注意这里只计算第三个轨迹的 return 为例,因为其是随机的:
如何去计算reward?对于下面的轨迹来说:
方法1:设 表示从 开始获得的return
方法2(Bootstrapping):
这种方法叫做自举,从自己出发得到自己,类似于递归
用矩阵来表示为:
可以简写为:
这就是确定性策略的贝尔曼公式,可以用线性代数求解此线性方程组
State Value
考虑以下单步过程:
:离散时间实例
:时间 的状态
:在状态 采取的动作
:采取 后获得的奖励
:采取 后转换到的状态
注意
都是随机变量。
这一步由以下概率分 ...